아래 문자는 네이버 블로그 검색 유입을 위해 위 사진의 글로 수식을 제외한 부분만 복사하여 붙여넣은 것입니다. 따라서 읽지 않아도 돼요.
네이버블로그수식편집기가한글문서의수식편집기보다더불편해서스마트에디터ONE의수식편집기는문장바로옆에수식을쓸수없기때문에어쩔수없이이렇게문장을쓰게되었습니다.12.3 편도함수(Partial Derivatives) 문제에서 특별한 언급 없이 의 1계 편도함수가 연속, 2계 편도함수가 연속이라는 조건을 부여할 수 있는데, 이는 모든 1계, 2계 편도함수가 연속이라는 뜻이다. 즉, 가 2 변수 함수일 때, 1계 편도 함수가 연속이면 가 모두 연속이고, 2계 편도 함수가 연속이면 가 모두 연속이다.Problem 12.3.1 때 값을 구하시오.sol) 모두에 대해서이기 때문에 편도함수의 정의에 따르면 말이다. ■Problem 12.3.2 때에 대해서만 부속 식으로 나타냅니다.sol) 편도함수의 정의에 따르면 다음을 얻는다.■Problem 12.3.2는 의 편도함수를 직접 구해 를 대입하고자 하면 계산이 복잡하다. 그러나 편도함수의 정의를 사용하면 계산량이 줄어들게 되는데, 그 이유는 이 때문이다.Problem 12.3.2와 같이 미분적분학에서의 을 계산할 때는, 이면 편도 함수의 정의를 사용해 계산하는 것이 용이한 경우가 많다.Problem 12.3에 대한 값을 구하시오.sol) 편도함수의 정의에 따르면 다음을 얻는다.따라서 편도함수의 정의에 따르면 다음을 얻을 수 있다.
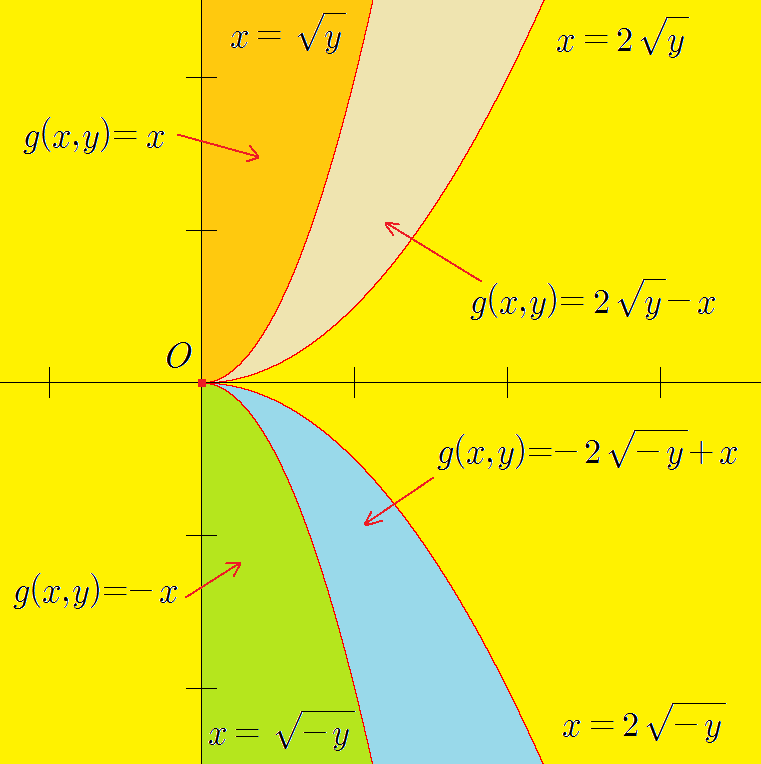
■Problem 12.3.3부터 실제로는 와인의 경우로 나누어 풀어야 한다. 실제로 극한파이며 분모에 포함되어 있기 때문이다. 하지만 그래서 편의상 케이스를 나누지 않고 계산하는 편이다.를 얻을 때도 같은 이유로 설명을 생략했다.Clairaut’s theorem에 따르면, Problem 12.3.3에서 주어진 함수에 대해 둘 중 적어도 하나는 에서 연속은 아님을 알 수 있지만, 실제로는 모든 것에서 불연속임을 증명해 보자.의 함수식은 분자, 분모 모두 다항식이므로, Clairaut’s의 원점에 의한 원점을 제외한 the mor’s의 원점에 의한 다항식이므로 Clairaut’s 그리고 Problem 12.3.3의 해석 과정을 그대로 따르면 시임을 쉽게 알 수 있다. 따라서 다음을 얻을 수 있다.따라서 다음을 얻는다.그래서 모든 것에 극한이란 존재하지 않는다. 따라서 모두 불연속이다.미분적분학에서 1계, 2계 편도함수가 에서 연속인지 아닌지 판정하는 문제를 풀 때에는 편도함수를 직접 계산하는 것보다는 Problem 12.3.3과 같이 편도함수의 정의를 사용하는 방향으로 접근하는 것이 용이한 경우가 많다.이를 위한 요령을 소개한다. 가 주어졌을 때 가부터 연속인지 불연속인지를 판정하는 문제를 풀 때, 우선 편도함수의 정의를 사용해 를 계산하는 것을 권장한다.마찬가지로 가로부터 연속인지 불연속인지를 판정하는 문제를 풀 때에도 편도함수의 정의를 이용해 를 먼저 계산하는 것을 권장한다.이 방법을 사용해서 다음 문제를 풀어 보자.Problem 12.3.4에 대해서, 「가」로부터 「연속」인가 「불연속」인가를 판정하시오.sol) 편도함수의 정의에 따르면 다음을 얻는다.따라서 ~지만 ~기 때문에 ~은)에서 불연속적이다. ■Problem 12.3.4에서 편도함수의 정의에 의하면, 이다. 따라서 가로부터 연속인지 판정하기 위해서는 편도함수를 직접 계산해야 한다. 직접 계산하면 다음을 얻을 수 있다.때문에 도의 불연속성을 알 수 있다.Problem 12.3.52 변수 함수는, 의 때 이하와 같이 정의되고 있다.이 때, 2 변수 함수를 다음과 같이 정의하자.의 함수 값을 몇 개 구해 보면 말이다.다음 물음에 답하시오.(a) 모든 것에 대한 것임을 증명하라.(b) 함수를 로 정의하자. 이면임을 증명하시오.sol)의 함수 값을 다음과 같이 좌표 평면상에 나타내자. 노란색으로 표시된 부분은 을 만족하는 영역이다.
(a). 그렇다면 모든 것에 대한 것이므로 편도함수의 정의에 따른다는 것을 쉽게 알 수 있다. 따라서 이때임을 증명하면 충분하다.그림을 보면 일할 때다. 앞으로가 앞으로에 가까워질 때가 어떻게 달라지는지 보자.「기 때문에」를 만족하는 「 ~」는 존재한다. 따라서 이 시점은 두 곡선 사이에 존재한다. 따라서 일 때문에가 충분히 작으면 를 만족하고 다음을 얻는다.
따라서, 모든 것에 대해서이다. ■(b)이면 모든 것에 대해서이므로 다음을 얻는다.뒷면이기 때문이다. 따라서 를 가정하자.case1)이 경우이기 때문이다. 그리고 뒷면이기 때문에 다음을 얻을 수 있다.
case 2)가 경우로, 주어진 범위에서 를 만족한다.그리고 이므로 case1에 따르면 이 성립한다. 따라서 다음을 얻는다.
그래서 이면이다. ■Problem 12.3.5이며 동시에 Problem 12.3.5에서 주어진 다음 등식의 반례가 된다.
미적분 (1) 또는 공학수학 (1)에서 편의상 1변수 함수를 나타내는 것을 배웠다. 편도함수도 유사하나, 2변수함수를 편의상 다음과 같이 제시한다.3 변수 함수에 대해서도 마찬가지로 편의상 다음과 같이 나타낸다.
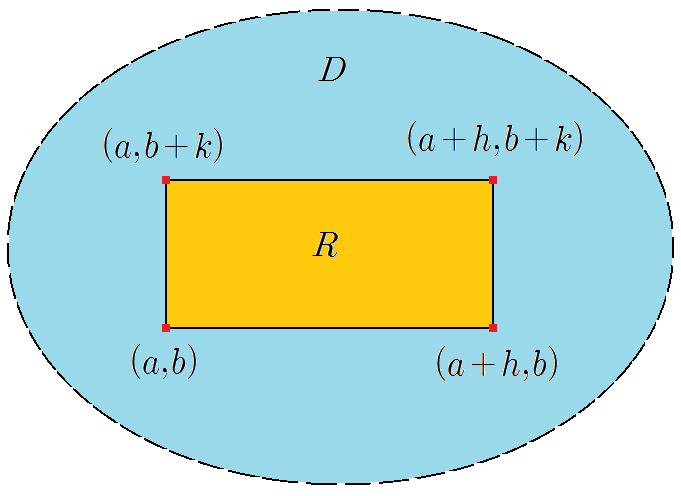
교재에서는 Clairaut’s theorem을 ” ” 가 모든 것을 포함한 적당한 Opendisk 위에서 연속적으로 있을 때 성립한다고 소개하지만, 실제로는 이보다 조금 약한 조건에서도 성립한다. 다음 문제를 풀어보자.Problem 12.3.6 함수에 대해 점을 포함한 Opendisk 위에서 연속이면 존재함을 증명하시오.sol)이 포함 Opendisk이기 때문에 다음 그림과 같이 네 점을 정점으로 하는 직사각형이 내부에 존재하는 것과 같은 오류가 존재한다.
그러면 “그럼”을 말할 때이므로 “Mean value theorem”에 따르면 다음을 만족하느냐 하는 사이에 존재하며 “Mean value theorem”을 다시 사용하면 를 만족하느냐 하는 사이에 존재한다. 이때는 에 의존하지 않는다
한편, 이라고 하면, 이므로 를 얻을 수 있다. 를 고정하고, 양변에 극한을 취하면, 위에서 연속하므로 다음을 얻는다.그래서 면이라는 것은 위에서부터 연속되므로 다음을 얻는다.따라서는 존재해서다. ■