엑셀로 T-Test를 하려면 분석 도구를 설치해야 해요설치 방법은 아래를 참고하시기 바랍니다.https://blog.naver.com/cndrud/221765903374 간단한 통계는 엑셀에서 사용이 가능합니다. SAS나 R, Python을 사용하지 않고도 간단한 통계 분석을 모두 해서… blog.naver.com
그럼 간단한 사례에 엑셀로 T-Test 할게요.
T-Test에 대한 설명은 아래를 참고하세요.https://blog.naver.com/cndrud/2217657108321 언제 쓰시나요? – 두 집단 간의 평균 차이가 통계적으로 의미가 있는지를 검증할 때 2. 검증… blog.naver.com
엑셀을 통한 T-Test 방법입니다.
예) A사의 타이어 수명과 B사의 타이어 수명이 동일한지를 비교(예제 Data.csv) 작업 절차에 따르면 01.자료 읽기 02. 기본통계량 확인03. 통계분석04. 자료 정리 및 시각화하지만 엑셀에서는 03. 통계분석 결과에 기본통계량이 나오므로 02. 기본통계량 확인은 생략해도 됩니다.
01.자료 가져오기 – 첨부된 자료를 클릭하여 열면 A 열에는 그룹 필드가 있고 B 열에는 타이어 수명이 있습니다.
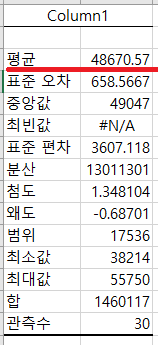
02. 기본 통계량 확인하기 엑셀 메뉴 ‘데이터’를 선택하고 ‘데이터 분석’을 클릭하면 ‘분석 도구’ 창이 나타납니다.- 겨울철 데이터 분석창이 뜨면 “기술통계법” 클릭 후 “확인” 클릭

확인을 누르면 아래와 같은 메뉴창이 다시 나타납니다. -“입력범위”에 일단 A사의 타이어수명데이터가 있는 영역을 선택하고 (입력범위 영역은 좁은 영역에 있는 위쪽 화살표를 클릭하면 마우스로 영역을 선택해주시면 편합니다.) -“요약통계량” 체크박스에 체크하여 확인클릭
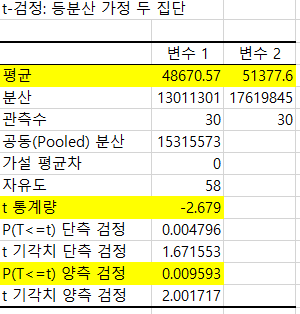
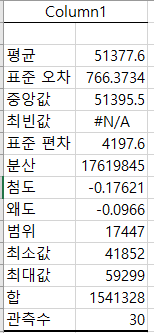
- 기술통계법은 간단한 기초통 계량이 계산되어 나옵니다. – 아래는 A사의 기술통계법 결과입니다.- 평균, 중앙값, 첨도, 왜도 등 기초 통계량이 나옵니다. – 즉, 여기서 확인할 수 있는 것은 A사의 타이어 수명 평균은 48,670 입니다.
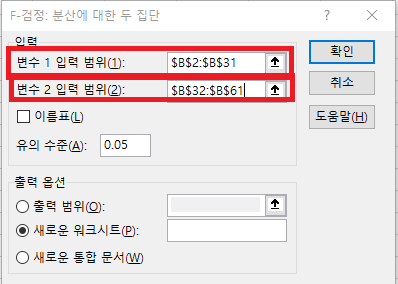
- 같은 방법으로 하면 B사의 기초 통계량은 다음과 같으며, B사의 타이어 수명은 평균 51,377입니다.

03. 통계분석 분석 목적에 맞는 테스트 모형을 선택해야 합니다.- 위 자료는 A사의 타이어 수명과 B사의 타이어 수명의 차이가 있는지 통계적으로 검증하는 것입니다. – 그러면 쌍체 비교 T-Test니까 독립적인 T-Test를 해주시면 됩니다
- 독립적인 T-Test는 먼저 두 집단의 분산이 같은지 다른지를 비교해야 합니다.(분산이 같은 경우와 분산이 다른 경우와 계산하는 방법이 다르기 때문에 “등분산 검증”부터 해야 합니다.)
- (1) 등분산 검증하는 방법 – 엑셀 메뉴 중 데이터 클릭 후 데이터 분석을 클릭하여 “F-검정: 분산에 대한 두 집단”을 선택하여 확인
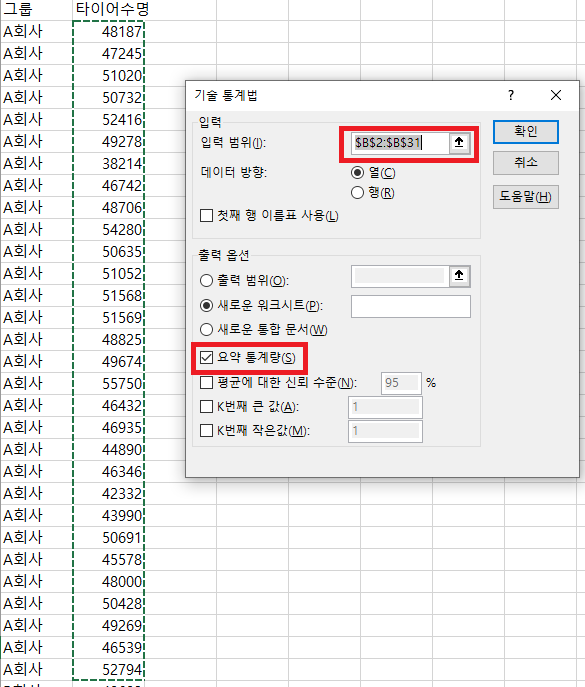
- 아래와 같이 입력창이 뜨면 변수 1 입력 범위에는 A사의 타이어 수명 데이터 영역 선택 변수 2 입력 범위에는 B사의 타이어 수명 데이터 영역 선택 후 확인 클릭
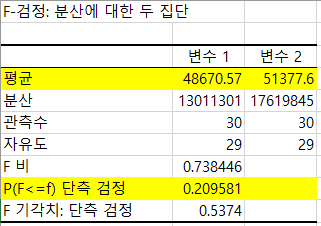
아래와 같이 등분산 검증 결과 값이 나타납니다.결과치가 나오면 노란색으로 칠해진 것만 보면 됩니다.변수 1(A사)의 평균 48,670, 변수 2(B사)의 평균 51,377입니다.그들의 분산이 같은 것에 대한 검증은 p-value라고 판단하시면 됩니다.이하의”P(F<=f) 단측 검증”치 0.2095 로서 0.05 보다 크기 때문에, A사와 B사의 분산은 차이가 없다고 말할 수 있습니다. (등분산 T-Test 사용) (통계Tip: p-value값을 간단하게 해석한 0.05보다 작으면 차이가 있고 크면 차이가 없다고 해석하시면 됩니다.)
(2) 등분산 T-Test- 이제부터는 원래 목적인 두 집단 간의 평균 차이가 있는지를 검증합니다.-“데이터 분석”을 클릭하면 “통계데이터 분석” 창이 뜨고-“t-검정: 등분산가정 두 집단” 선택 후 확인

- 변수 1에 A사 타이어 수명 데이터 선택 – 변수 2에 B사 타이어 수명 데이터 선택 (아까와 비슷하죠?) 엑셀의 통계 분석 입력 창 양식은 거의 비슷합니다.)
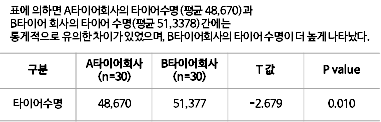
- 등분산 T-Test 결과는 다음과 같이 나옵니다.- 역시 여기도 평균이 나오고, T 통계량도 나오고, p-value 값도 나옵니다. – “P(T<=t) 양측 검증” 값이 0.0095로 0.05보다 작기 때문에 두 집단의 평균에는 차이가 있다고 결론지을 수 있습니다.

04. 자료 정리 및 시각화- 이 부분은 다양하게 할 수 있지만… 아래와 같이 설명하시면 됩니다.
생각보다 길어졌네요.여기서 등분산검정하고 결론이 분산이 다르다고 나오면

음의 표에서 “t-검증:이분산가정 두 집단”을 선택하세요.독립 표본이 아닌 쌍체 비교의 경우는, 다이어트 전후의 체중차이나 작년과 금년의 성적차등의 쌍체 비교에서는, 「t-검정:쌍체 비교」를 선택해 주세요.그 이후로는 같습니다.결과도 똑같이 해석하시면 됩니다
마지막으로귀무가설,채택,기각,이런이야기를안한이유는이렇게얘기를시작하면큰일이날것같아요.그래서쉽게p-value값만보고0.05보다작으면차이가있다.0.05보다 크면 차이가 없다.이렇게 이해하는게 훨씬 쉽게 이해될 것 같아서 이런 방법으로 알려드립니다.